문제
https://www.acmicpc.net/problem/16928
16928번: 뱀과 사다리 게임
첫째 줄에 게임판에 있는 사다리의 수 N(1 ≤ N ≤ 15)과 뱀의 수 M(1 ≤ M ≤ 15)이 주어진다. 둘째 줄부터 N개의 줄에는 사다리의 정보를 의미하는 x, y (x < y)가 주어진다. x번 칸에 도착하면, y번 칸으
www.acmicpc.net
개요
처음 문제를 봤을 때 어떻게 구현해야 할지 감이 바로 오지 않았다.
10 x 10 크기의 100칸짜리 보드판이 주어졌기 때문에, 10 x 10 의 2차원 배열을 만들어야 하는 것인가 생각했다.
왜냐하면, 이 문제가 그래프 카테고리에 있었기 때문에 DFS 또는 BFS를 사용하는 문제일텐데, 궁극적으로 목적지까지의 최소 거리를 구하는 문제이므로 BFS를 사용해야 할 것이라고 추측했고, 이전에 풀어봤던 BFS 문제들은 대부분 2차원 배열 형태의 좌표 형식의 문제였기 때문에 자연스럽게 2차원 배열로 접근해야 할 것이라고 생각했다.
그러나, 굳이 2차원 배열을 만들 필요 없이 1부터 100까지의 숫자를 담을 수 있는 길이 101짜리 1차원 배열이면 충분하다.
만약, 예를 들어 3 x 3 크기의 9칸짜리 보드판이 있다고 해보자.
그리고, 사다리는 2 → 8, 뱀은 7 → 5, 5 → 3 이 존재한다고 하자.
2차원 배열로 보드판을 표현하면 다음과 같다.
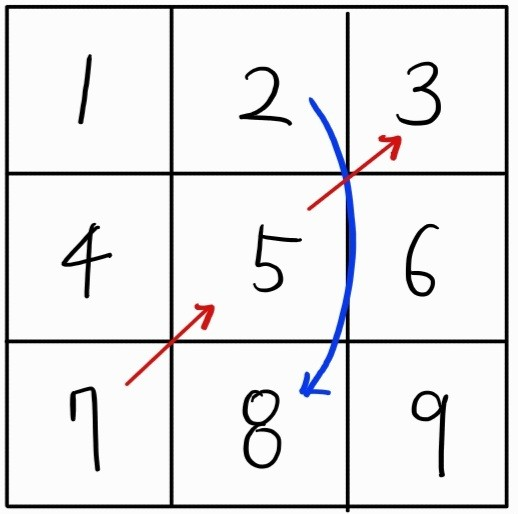
반면, 1차원 배열로 보드판을 표현하면 다음과 같다.
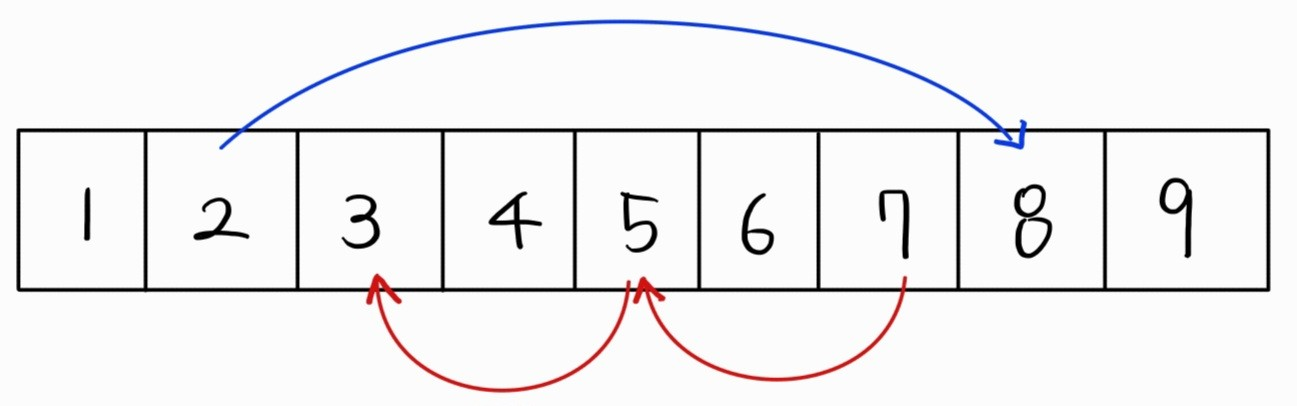
사실상 그림만 보더라도, 1차원 배열로 생각하는 것이 훨씬 보기 편할 뿐더러, 구현하기 편할 것이라는 것을 알 수 있다.
일차원 배열에서의 연결 관계를 바탕으로 만든 그래프는 다음과 같다.
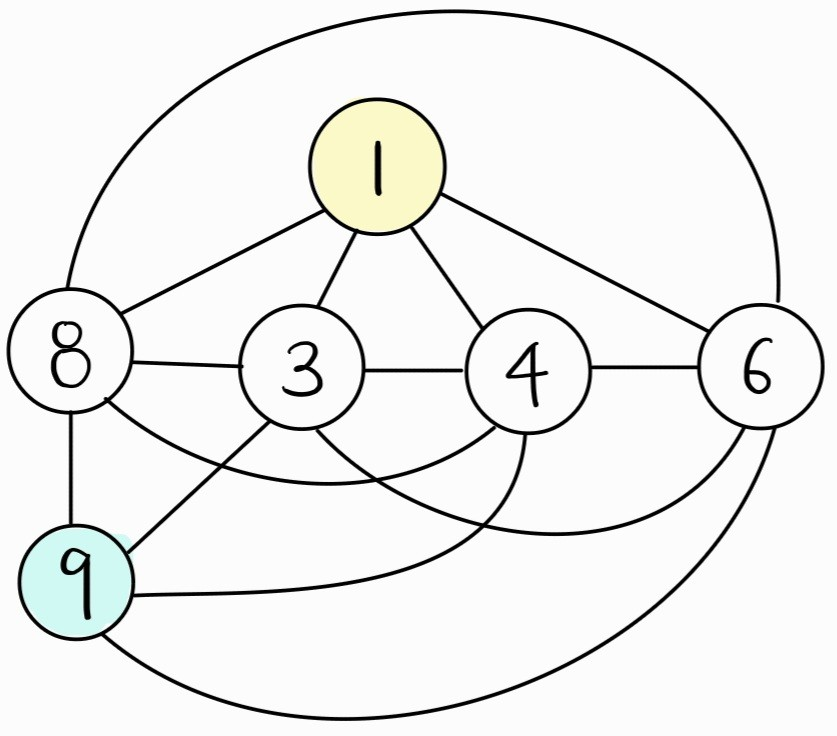
즉, 그래프 상에서 출발지가 1이고, 목적지가 9일 때, 목적지까지 도달하기 위한 최단 거리를 구하는 문제와 동일한 것이다.
사실, 이 문제가 그래프 카테고리에 있지 않았다면, BFS로 풀 생각을 바로 떠올리지는 못 했을 것 같다.
오히려, DP로 접근했을 것 같다.
사다리만 있었다면 DP로 구현이 가능했을 것 같은데, 뱀을 통해 더 작은 숫자로 돌아올 수 있는 상황 때문에 DP는 사실상 구현이 굉장히 어려울 것 같다.
코드
#include <iostream>
#include <cstring>
#include <sstream>
#include <vector>
#include <deque>
#include <queue>
#include <map>
#include <algorithm>
#include <bitset>
#include <cstdio>
using namespace std;
int board[101]; // 각 위치에 뱀 or 사다리 있는 경우 다음 위치 저장
int dist[101]; // 각 위치에 도달할 수 있는 최소 이동 횟수
void bfs(int start) {
queue <int> q;
q.push(start);
while (!q.empty()) {
int x = q.front();
q.pop();
for (int i = 1; i <= 6; i++) {
int nx = x + i;
if (nx > 100) continue;
if (dist[nx] != 0) continue;
// while문을 쓴 이유는 뱀 or 사다리 타고 이동한 위치에 또 뱀 or 사다리가 있는 경우 고려
while (board[nx] != 0) { // nx 위치에 사다리나 뱀이 있는 경우
nx = board[nx]; // nx 위치로 이동
}
if (dist[nx] == 0) {
dist[nx] = dist[x] + 1;
q.push(nx);
}
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n, m; cin >> n >> m;
for (int i = 0; i < n; i++) {
int x, y; cin >> x >> y;
board[x] = y;
}
for (int i = 0; i < m; i++) {
int u, v; cin >> u >> v;
board[u] = v;
}
bfs(1);
cout << dist[100];
return 0;
}
일차원 배열 board는 각 위치에 뱀 or 사다리 있는 경우 뱀 or 사다리를 통해 이동하게 되는 다음 위치를 저장한다.
예를 들어, 5번 칸에 사다리가 있고, 사다리를 통해 20번 칸으로 이동하게 된다면 board[5] = 20인 것이다.
만약, 뱀 or 사다리가 없는 위치에는 0이 저장되어 있다.
일차원 배열 dist는 각 위치에 도달할 수 있는 최소 이동 횟수를 저장한다.
예를 들어, 50번 칸에 도달할 수 있는 최소 이동 횟수가 3회라면, dist[50] = 3이다.
bfs 함수는 따로 분리해서 구현해주었다.
bfs는 dfs와 달리 재귀를 사용하지 않기 때문에 main 함수에서 바로 구현할 수 있으나, 따로 함수를 만들어 구현하는 것이 가독성이 좋다고 생각했다.
bfs 함수의 첫 부분은 기존의 bfs 함수와 동일하다.
주사위의 결과에 따라 1칸부터 6칸까지 이동할 수 있기 때문에 i 값을 1부터 6까지 증가시키며 사용하는 for문을 사용했다.
중요한 부분은 다음 코드이다.
while (board[nx] != 0) { // nx 위치에 사다리나 뱀이 있는 경우
nx = board[nx]; // nx 위치로 이동
}단순히 if 문이 아니라, while 문을 사용한 이유는 뱀 or 사다리를 타고 이동한 다음 위치에 또 뱀 or 사다리가 있는 경우에는 또 한 번 그 다음 위치로 넘어가게 되는 경우를 고려해준 것이다.
그리고, dist[nx]가 0인 경우, 즉 아직 방문하지 않은 위치인 경우에만 dist[nx]에 이전 위치인 x에서의 dist[x]에서 1을 더해준 값을 저장한다.
dist[nx]가 0이 아닌 경우는 즉 이미 방문을 한 경우이기 때문에 dist[nx]에 이미 최소 이동 횟수가 저장되어 있는 것이다.
그리고 nx를 queue에 push해준다.
깨달은 점
일단, 그래프 문제를 굉장히 오랜만에 풀어서 bfs 함수를 떠올리는데도 조금 시간이 걸렸다.
기존에는, 이차원 좌표가 주어져서 동서남북 4방향으로 이동하거나, 한 노드에 어떤 노드가 연결되어 있는지의 정보가 주어지는 형태의 그래프 문제를 많이 풀어보았다.
이 문제는 기존에 풀었던 문제들과 약간 다른 스타일이어서 좀 고전했던 것 같다.
그래프 문제는 풀이를 알고나면 생각보다 쉬운데, 그 풀이를 떠올리기가 쉽지 않은 것 같다.
그래프 문제를 많이 풀면서 많은 유형을 익히는 수 밖에 없겠다.
'백준 문제 리뷰 > 그래프' 카테고리의 다른 글
| [백준 1504] 특정한 최단 경로 (C++) - G4 (3) | 2023.09.29 |
|---|---|
| [백준 7576] 토마토 (BFS) (C++) (1) | 2023.01.12 |
문제
https://www.acmicpc.net/problem/16928
16928번: 뱀과 사다리 게임
첫째 줄에 게임판에 있는 사다리의 수 N(1 ≤ N ≤ 15)과 뱀의 수 M(1 ≤ M ≤ 15)이 주어진다. 둘째 줄부터 N개의 줄에는 사다리의 정보를 의미하는 x, y (x < y)가 주어진다. x번 칸에 도착하면, y번 칸으
www.acmicpc.net
개요
처음 문제를 봤을 때 어떻게 구현해야 할지 감이 바로 오지 않았다.
10 x 10 크기의 100칸짜리 보드판이 주어졌기 때문에, 10 x 10 의 2차원 배열을 만들어야 하는 것인가 생각했다.
왜냐하면, 이 문제가 그래프 카테고리에 있었기 때문에 DFS 또는 BFS를 사용하는 문제일텐데, 궁극적으로 목적지까지의 최소 거리를 구하는 문제이므로 BFS를 사용해야 할 것이라고 추측했고, 이전에 풀어봤던 BFS 문제들은 대부분 2차원 배열 형태의 좌표 형식의 문제였기 때문에 자연스럽게 2차원 배열로 접근해야 할 것이라고 생각했다.
그러나, 굳이 2차원 배열을 만들 필요 없이 1부터 100까지의 숫자를 담을 수 있는 길이 101짜리 1차원 배열이면 충분하다.
만약, 예를 들어 3 x 3 크기의 9칸짜리 보드판이 있다고 해보자.
그리고, 사다리는 2 → 8, 뱀은 7 → 5, 5 → 3 이 존재한다고 하자.
2차원 배열로 보드판을 표현하면 다음과 같다.

반면, 1차원 배열로 보드판을 표현하면 다음과 같다.

사실상 그림만 보더라도, 1차원 배열로 생각하는 것이 훨씬 보기 편할 뿐더러, 구현하기 편할 것이라는 것을 알 수 있다.
일차원 배열에서의 연결 관계를 바탕으로 만든 그래프는 다음과 같다.

즉, 그래프 상에서 출발지가 1이고, 목적지가 9일 때, 목적지까지 도달하기 위한 최단 거리를 구하는 문제와 동일한 것이다.
사실, 이 문제가 그래프 카테고리에 있지 않았다면, BFS로 풀 생각을 바로 떠올리지는 못 했을 것 같다.
오히려, DP로 접근했을 것 같다.
사다리만 있었다면 DP로 구현이 가능했을 것 같은데, 뱀을 통해 더 작은 숫자로 돌아올 수 있는 상황 때문에 DP는 사실상 구현이 굉장히 어려울 것 같다.
코드
#include <iostream>
#include <cstring>
#include <sstream>
#include <vector>
#include <deque>
#include <queue>
#include <map>
#include <algorithm>
#include <bitset>
#include <cstdio>
using namespace std;
int board[101]; // 각 위치에 뱀 or 사다리 있는 경우 다음 위치 저장
int dist[101]; // 각 위치에 도달할 수 있는 최소 이동 횟수
void bfs(int start) {
queue <int> q;
q.push(start);
while (!q.empty()) {
int x = q.front();
q.pop();
for (int i = 1; i <= 6; i++) {
int nx = x + i;
if (nx > 100) continue;
if (dist[nx] != 0) continue;
// while문을 쓴 이유는 뱀 or 사다리 타고 이동한 위치에 또 뱀 or 사다리가 있는 경우 고려
while (board[nx] != 0) { // nx 위치에 사다리나 뱀이 있는 경우
nx = board[nx]; // nx 위치로 이동
}
if (dist[nx] == 0) {
dist[nx] = dist[x] + 1;
q.push(nx);
}
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n, m; cin >> n >> m;
for (int i = 0; i < n; i++) {
int x, y; cin >> x >> y;
board[x] = y;
}
for (int i = 0; i < m; i++) {
int u, v; cin >> u >> v;
board[u] = v;
}
bfs(1);
cout << dist[100];
return 0;
}
일차원 배열 board는 각 위치에 뱀 or 사다리 있는 경우 뱀 or 사다리를 통해 이동하게 되는 다음 위치를 저장한다.
예를 들어, 5번 칸에 사다리가 있고, 사다리를 통해 20번 칸으로 이동하게 된다면 board[5] = 20인 것이다.
만약, 뱀 or 사다리가 없는 위치에는 0이 저장되어 있다.
일차원 배열 dist는 각 위치에 도달할 수 있는 최소 이동 횟수를 저장한다.
예를 들어, 50번 칸에 도달할 수 있는 최소 이동 횟수가 3회라면, dist[50] = 3이다.
bfs 함수는 따로 분리해서 구현해주었다.
bfs는 dfs와 달리 재귀를 사용하지 않기 때문에 main 함수에서 바로 구현할 수 있으나, 따로 함수를 만들어 구현하는 것이 가독성이 좋다고 생각했다.
bfs 함수의 첫 부분은 기존의 bfs 함수와 동일하다.
주사위의 결과에 따라 1칸부터 6칸까지 이동할 수 있기 때문에 i 값을 1부터 6까지 증가시키며 사용하는 for문을 사용했다.
중요한 부분은 다음 코드이다.
while (board[nx] != 0) { // nx 위치에 사다리나 뱀이 있는 경우
nx = board[nx]; // nx 위치로 이동
}단순히 if 문이 아니라, while 문을 사용한 이유는 뱀 or 사다리를 타고 이동한 다음 위치에 또 뱀 or 사다리가 있는 경우에는 또 한 번 그 다음 위치로 넘어가게 되는 경우를 고려해준 것이다.
그리고, dist[nx]가 0인 경우, 즉 아직 방문하지 않은 위치인 경우에만 dist[nx]에 이전 위치인 x에서의 dist[x]에서 1을 더해준 값을 저장한다.
dist[nx]가 0이 아닌 경우는 즉 이미 방문을 한 경우이기 때문에 dist[nx]에 이미 최소 이동 횟수가 저장되어 있는 것이다.
그리고 nx를 queue에 push해준다.
깨달은 점
일단, 그래프 문제를 굉장히 오랜만에 풀어서 bfs 함수를 떠올리는데도 조금 시간이 걸렸다.
기존에는, 이차원 좌표가 주어져서 동서남북 4방향으로 이동하거나, 한 노드에 어떤 노드가 연결되어 있는지의 정보가 주어지는 형태의 그래프 문제를 많이 풀어보았다.
이 문제는 기존에 풀었던 문제들과 약간 다른 스타일이어서 좀 고전했던 것 같다.
그래프 문제는 풀이를 알고나면 생각보다 쉬운데, 그 풀이를 떠올리기가 쉽지 않은 것 같다.
그래프 문제를 많이 풀면서 많은 유형을 익히는 수 밖에 없겠다.
'백준 문제 리뷰 > 그래프' 카테고리의 다른 글
| [백준 1504] 특정한 최단 경로 (C++) - G4 (3) | 2023.09.29 |
|---|---|
| [백준 7576] 토마토 (BFS) (C++) (1) | 2023.01.12 |
