최단 경로(Shortest Path) 알고리즘
- 다익스트라(Dijkstra)
- 벨만-포드(Bellman-Ford)
- 플로이드-와샬(Floyd-Warshall)
다익스트라(Dijkstra) 알고리즘이란?
다익스트라 알고리즘은 최단경로(Shortest Path) 알고리즘 중의 하나입니다.
더 정확히는, 그래프의 한 정점에서 다른 정점들까지의 최단 거리를 구하는 알고리즘입니다.
다만, 가중치의 값이 음수인 간선이 존재하는 경우에는 다익스트라 알고리즘을 사용할 수 없습니다. (이 경우에는 벨만-포드 알고리즘을 사용해야 합니다.)
즉, 다익스트라 알고리즘은 간선의 가중치가 모두 0 또는 양수인 경우에만 사용 가능합니다.
다익스트라 알고리즘의 로직은 다음과 같습니다.
1. 출발 정점을 설정한다.
2. 출발 정점와 인접해있는 정점들까지의 거리를 갱신한다.
3. 아직 방문하지 않은 정점들 중 기록된 거리가 가장 짧은 정점 u를 하나 선택하여 방문한다.
(u를 선택할 때, 꼭 현재 정점과 인접한 정점이 아니어도 상관 없다. 멀리 떨어져있는 정점이라도 dist 값이 가장 작은 정점을 선택한다.)
4. 해당 정점 u와 인접하고 아직 방문하지 않은 정점들까지의 거리를 갱신한다.
(해당 정점을 거쳐서 방문할 수 있는 정점까지의 거리가 이전에 기록된 값보다 작다면 그 거리를 갱신한다.)
5. 3과 4를 반복한다.
예시를 통해 그 과정을 더 자세히 살펴보도록 하자.
다음과 같은 그래프가 있다.
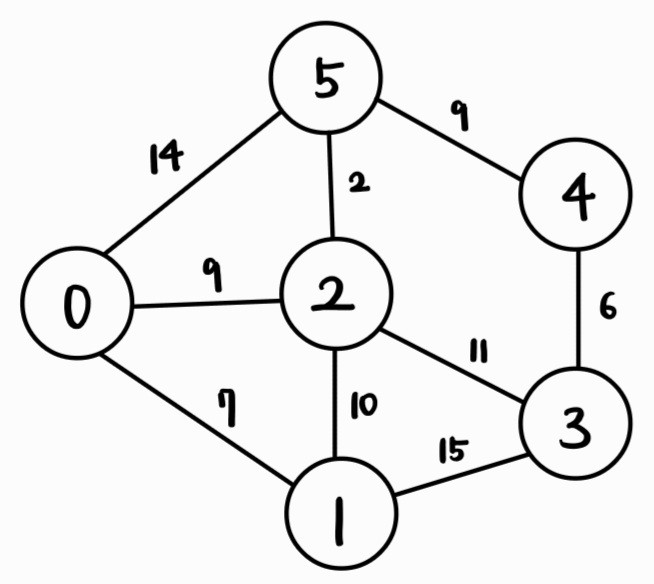
시작 정점은 0번이라고 가정하자.
그리고, 일차원 배열 dist에 각 정점까지의 최단거리를 저장할 것이다.
처음에는 각 정점까지의 거리를 모두 INF로 초기화한다.
| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | INF | INF | INF | INF | INF | INF |
| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | INF | INF | INF | INF | INF |
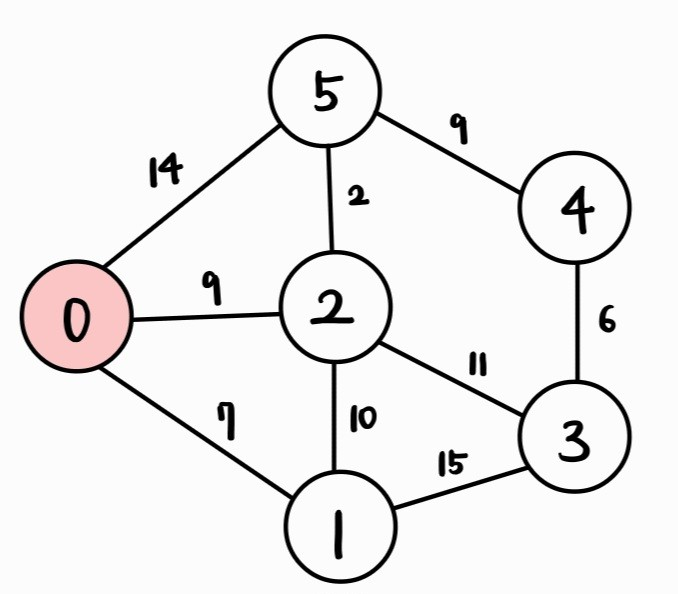
- 시작 정점인 0을 방문한다.
- 시작 정점인 0에 대한 dist 배열 값을 0으로 설정한다.
| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | 7 | 9 | INF | INF | 14 |
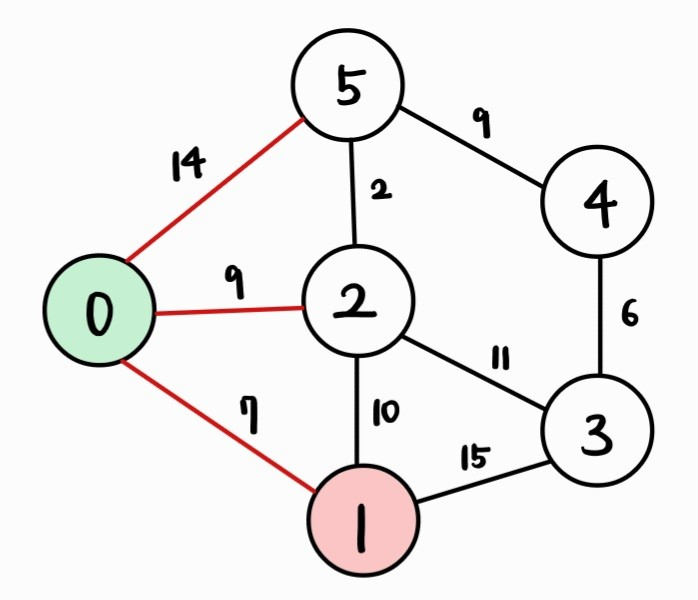
- 0번 정점과 인접하면서 아직 방문하지 않은 정점인 1, 2, 5번 정점까지의 거리를 갱신한다.
→ 0번 정점을 거쳐서 k번 정점으로 가는 거리인 dist[0] + cost[0][k]가 dist[k]보다 작으면 갱신한다.
- 아직 방문하지 않은 정점 중 거리(dist 배열 값)가 가장 짧은 1번 정점을 방문한다.
| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | 7 | 9 | 22 | INF | 14 |
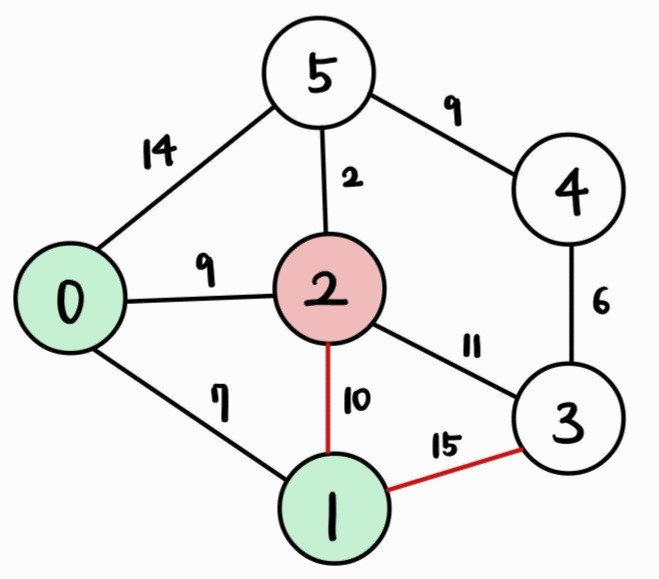
- 1번 정점과 인접하면서 아직 방문하지 않은 정점인 2, 3번 정점까지의 거리를 갱신한다.
→ 1번 정점을 거쳐서 k번 정점으로 가는 거리인 dist[1] + cost[1][k]가 dist[k]보다 작으면 갱신한다.
- 사실, dist[1] + cost[1][2] = 17 > 9 = dist[2] 이므로 2번 정점까지의 거리(dist[2])는 갱신하지 않는다.
- 즉, 3번 정점까지의 거리(dist[3])만 갱신한다.
- 그리고, 아직 방문하지 않은 정점 중 거리(dist 배열 값)가 가장 짧은 2번 정점을 방문한다.
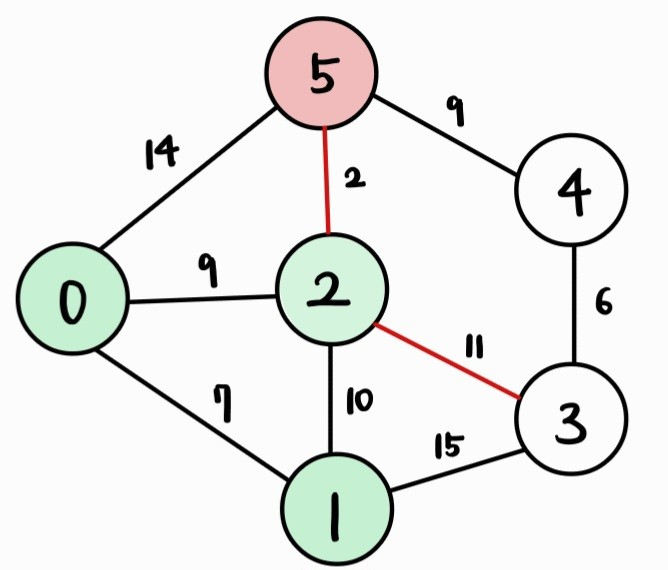
| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | 7 | 9 | 20 | INF | 11 |
- 2번 정점과 인접하면서 아직 방문하지 않은 정점인 3, 5번 정점까지의 거리를 갱신한다.
→ 2번 정점을 거쳐서 k번 정점으로 가는 거리인 dist[2] + cost[2][k]가 dist[k]보다 작으면 갱신한다.
- 아직 방문하지 않은 정점 중 거리(dist 배열 값)가 가장 짧은 5번 정점을 방문한다.
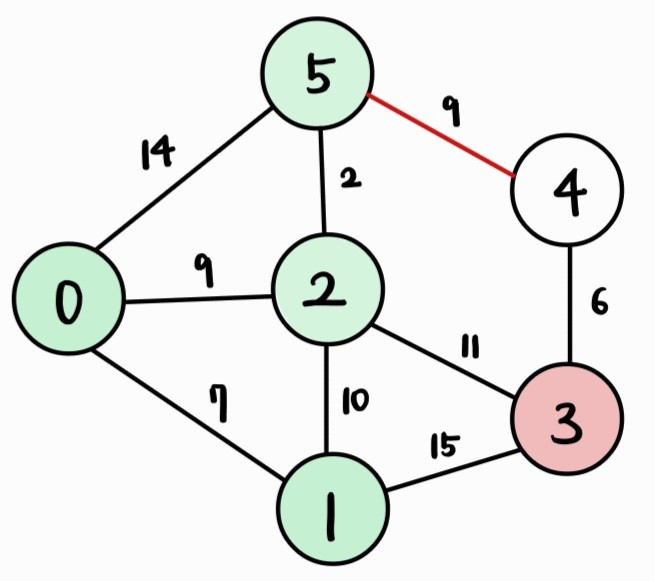
| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | 7 | 9 | 20 | 20 | 11 |
- 5번 정점과 인접하면서 아직 방문하지 않은 정점인 4번 정점까지의 거리를 갱신한다.
→ 5번 정점을 거쳐서 k번 정점으로 가는 거리인 dist[5] + cost[5][k]가 dist[k]보다 작으면 갱신한다.
- 아직 방문하지 않은 정점 중 거리(dist 배열 값)가 가장 짧은 3번 정점을 방문한다.
→ dist[3]과 dist[4]의 값이 20으로 동일하기 때문에 둘 중 아무 정점이나 방문해도 상관 없다.
→ 꼭 5번 정점과 인접한 4번 정점을 방문할 필요는 없다. 3번 정점을 방문해도 상관 없다.
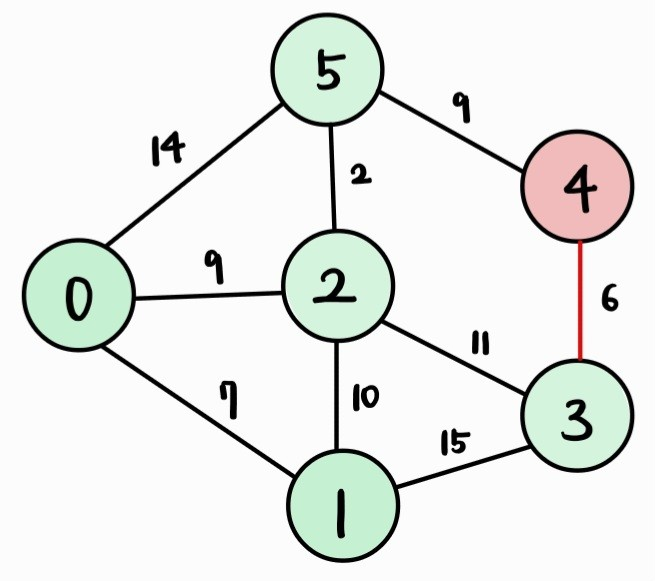
| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | 7 | 9 | 20 | 20 | 11 |
- 3번 정점과 인접하면서 아직 방문하지 않은 정점인 4번 정점까지의 거리를 갱신한다.
→ 3번 정점을 거쳐서 k번 정점으로 가는 거리인 dist[3] + cost[3][k]가 dist[k]보다 작으면 갱신한다.
- 사실, dist[3] + cost[3][4] = 26 > 20 = dist[4] 이므로 4번 정점까지의 거리(dist[4])는 갱신하지 않는다.
- 즉, 어떤 값도 갱신하지 않는다.
- 아직 방문하지 않은 정점 중 거리(dist 배열 값)가 가장 짧은 4번 정점을 방문한다.
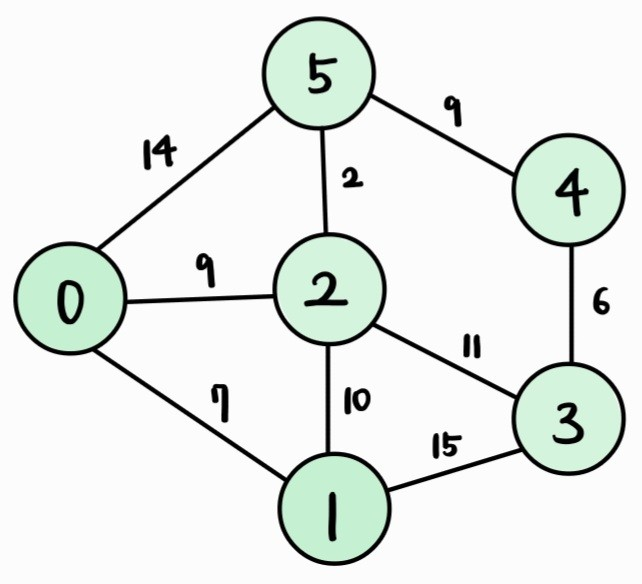
| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | 7 | 9 | 20 | 20 | 11 |
모든 정점을 방문했기 때문에 아무 것도 하지 않고 마무리한다.
다익스트라(Dijkstra) 알고리즘 코드 (C++)
#include <iostream>
#include <cstring>
#include <sstream>
#include <vector>
#include <deque>
#include <queue>
#include <map>
#include <algorithm>
#include <bitset>
#include <cmath>
#define INF (~0U >> 2) // 약 10억 7천만 (1073741823)
using namespace std;
int v, e, k; // 정점 개수, 간선 개수, 시작 정점
vector<pair<int, int>> adj[20001]; // 인접 리스트 (인접한 정점과 그 정점까지의 거리를 저장)
vector<int> dist(20001, INF);
// 우선순위 큐
// 큰 원소부터 pop : priority_queue<int> pq;
// 작은 원소부터 pop : priority_queue<int, vector<int>, greater<int>> pq;
void dijkstra(int start) { // start는 시작 정점
dist[start] = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq; // ({dist[k], k} 저장)
pq.push({ dist[k], k });
while (!pq.empty()) {
int cur_dist = pq.top().first;
int cur = pq.top().second;
pq.pop();
// 이미 방문한 정점은 무시 (이미 방문한 정점의 dist 값은 가장 최소인 상태)
if (dist[cur] < cur_dist) continue;
for (auto k : adj[cur]) {
int next_dist = k.first;
int next = k.second;
// 현재 정점을 거쳐서 인접 정점을 방문하는 것이 더 거리가 짧은 경우
// <=> dist[cur] + adj[cur][next] < dist[next]
if (cur_dist + next_dist < dist[next]) {
// 거리 갱신
dist[next] = cur_dist + next_dist;
pq.push({ dist[next], next });
}
}
}
}
int main(void) {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> v >> e >> k;
for (int i = 0; i < e; i++) {
int a, b, c; cin >> a >> b >> c;
adj[a].push_back({ c, b });
}
dijkstra(k);
for (int i = 1; i <= v; i++) {
if (dist[i] == INF) cout << "INF\n";
else cout << dist[i] << '\n';
}
return 0;
}위 코드는 백준 1753번 [최단 경로] 문제의 해답 코드이다.
https://www.acmicpc.net/problem/1753
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net
주의할 점
[주의점 1]
priority_queue의 원소로 pair<int, int>를 사용할 때 따로 비교 함수를 지정해주지 않는다면 first를 기준으로 정렬된다.
다익스트라 알고리즘에서는 priority_queue에서 정점 k에 대한 dist[k] 값이 여러 번 갱신된다면 priority_queue에 {dist[k], k} 쌍이 여러 개 존재할 수 있다.
그 여러 쌍 중에서, dist[k] 값이 작은 것이 더 앞으로 가도록 하기 때문에, 정렬 기준이 되는 dist 값을 first 위치에 두어야 한다.
pq.push({ dist[next], next });
그리고, dist[k] 값이 가장 작은 {dist[k], k} 쌍이 선택되어 정점 k에 방문하면, 말 그대로 dist[k] 값은 가능한 가장 최소의 값을 가지고 있는 상태이다.
그런데, priority_queue에 이제는 필요없는 {dist[k], k} 쌍들이 남아있을 수 있기 때문에, 이 쌍들을 무시하기 위해 다음과 같은 코드를 작성해주어야 한다.
if (dist[cur] < cur_dist) continue;
[주의점 2]
vector에서 큰 원소부터 접근하기 위해서는 내림차순 정렬 sort(v.begin(), v.end(), greater<>())을 하고,
작은 원소부터 접근하기 위해서는 오름차순 정렬 sort(v.begin(), v.end())을 한다.
비슷한 방식으로,
우선순위 큐에서 큰 원소부터 pop하기 위해서는 priority_queue<int> pq를 하고,
작은 원소부터 pop하기 위해서는 priority_queue<int, vector<int>, greater<int>> pq를 한다.
다음과 같이 이해하면 쉽게 기억할 수 있을 것이다.
vector는기존 그대로 생각하면 된다.
sort(v.begin(), v.end())를 하면 맨 앞에서부터, 즉 가장 작은 원소부터 접근하게 된다.
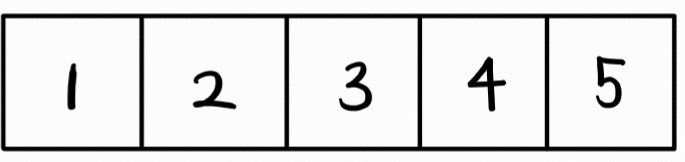
priority_queue는 vector를 세로로 세워서 생각하면 편하다.
그리고 맨 위에서부터 원소에 접근한다고 생각하면 된다.
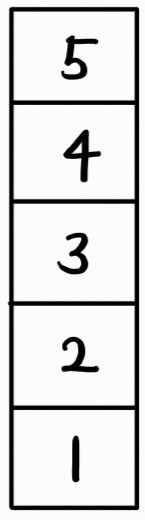
즉, priority_queue<int> pq를 사용하면 우선 순위 큐에서 가장 큰 수부터 pop할 수 있다.
즉, vector와 priority_queue는 반대로 접근하면 된다.
'알고리즘 정리' 카테고리의 다른 글
| PS 문제 풀이 일지 (~ing) (0) | 2023.07.30 |
|---|---|
| 문자열 split 방법 (isstringstream 사용) (0) | 2023.05.12 |
최단 경로(Shortest Path) 알고리즘
- 다익스트라(Dijkstra)
- 벨만-포드(Bellman-Ford)
- 플로이드-와샬(Floyd-Warshall)
다익스트라(Dijkstra) 알고리즘이란?
다익스트라 알고리즘은 최단경로(Shortest Path) 알고리즘 중의 하나입니다.
더 정확히는, 그래프의 한 정점에서 다른 정점들까지의 최단 거리를 구하는 알고리즘입니다.
다만, 가중치의 값이 음수인 간선이 존재하는 경우에는 다익스트라 알고리즘을 사용할 수 없습니다. (이 경우에는 벨만-포드 알고리즘을 사용해야 합니다.)
즉, 다익스트라 알고리즘은 간선의 가중치가 모두 0 또는 양수인 경우에만 사용 가능합니다.
다익스트라 알고리즘의 로직은 다음과 같습니다.
1. 출발 정점을 설정한다.
2. 출발 정점와 인접해있는 정점들까지의 거리를 갱신한다.
3. 아직 방문하지 않은 정점들 중 기록된 거리가 가장 짧은 정점 u를 하나 선택하여 방문한다.
(u를 선택할 때, 꼭 현재 정점과 인접한 정점이 아니어도 상관 없다. 멀리 떨어져있는 정점이라도 dist 값이 가장 작은 정점을 선택한다.)
4. 해당 정점 u와 인접하고 아직 방문하지 않은 정점들까지의 거리를 갱신한다.
(해당 정점을 거쳐서 방문할 수 있는 정점까지의 거리가 이전에 기록된 값보다 작다면 그 거리를 갱신한다.)
5. 3과 4를 반복한다.
예시를 통해 그 과정을 더 자세히 살펴보도록 하자.
다음과 같은 그래프가 있다.

시작 정점은 0번이라고 가정하자.
그리고, 일차원 배열 dist에 각 정점까지의 최단거리를 저장할 것이다.
처음에는 각 정점까지의 거리를 모두 INF로 초기화한다.
| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | INF | INF | INF | INF | INF | INF |

| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | INF | INF | INF | INF | INF |
- 시작 정점인 0을 방문한다.
- 시작 정점인 0에 대한 dist 배열 값을 0으로 설정한다.

| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | 7 | 9 | INF | INF | 14 |
- 0번 정점과 인접하면서 아직 방문하지 않은 정점인 1, 2, 5번 정점까지의 거리를 갱신한다.
→ 0번 정점을 거쳐서 k번 정점으로 가는 거리인 dist[0] + cost[0][k]가 dist[k]보다 작으면 갱신한다.
- 아직 방문하지 않은 정점 중 거리(dist 배열 값)가 가장 짧은 1번 정점을 방문한다.

| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | 7 | 9 | 22 | INF | 14 |
- 1번 정점과 인접하면서 아직 방문하지 않은 정점인 2, 3번 정점까지의 거리를 갱신한다.
→ 1번 정점을 거쳐서 k번 정점으로 가는 거리인 dist[1] + cost[1][k]가 dist[k]보다 작으면 갱신한다.
- 사실, dist[1] + cost[1][2] = 17 > 9 = dist[2] 이므로 2번 정점까지의 거리(dist[2])는 갱신하지 않는다.
- 즉, 3번 정점까지의 거리(dist[3])만 갱신한다.
- 그리고, 아직 방문하지 않은 정점 중 거리(dist 배열 값)가 가장 짧은 2번 정점을 방문한다.

| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | 7 | 9 | 20 | INF | 11 |
- 2번 정점과 인접하면서 아직 방문하지 않은 정점인 3, 5번 정점까지의 거리를 갱신한다.
→ 2번 정점을 거쳐서 k번 정점으로 가는 거리인 dist[2] + cost[2][k]가 dist[k]보다 작으면 갱신한다.
- 아직 방문하지 않은 정점 중 거리(dist 배열 값)가 가장 짧은 5번 정점을 방문한다.

| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | 7 | 9 | 20 | 20 | 11 |
- 5번 정점과 인접하면서 아직 방문하지 않은 정점인 4번 정점까지의 거리를 갱신한다.
→ 5번 정점을 거쳐서 k번 정점으로 가는 거리인 dist[5] + cost[5][k]가 dist[k]보다 작으면 갱신한다.
- 아직 방문하지 않은 정점 중 거리(dist 배열 값)가 가장 짧은 3번 정점을 방문한다.
→ dist[3]과 dist[4]의 값이 20으로 동일하기 때문에 둘 중 아무 정점이나 방문해도 상관 없다.
→ 꼭 5번 정점과 인접한 4번 정점을 방문할 필요는 없다. 3번 정점을 방문해도 상관 없다.

| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | 7 | 9 | 20 | 20 | 11 |
- 3번 정점과 인접하면서 아직 방문하지 않은 정점인 4번 정점까지의 거리를 갱신한다.
→ 3번 정점을 거쳐서 k번 정점으로 가는 거리인 dist[3] + cost[3][k]가 dist[k]보다 작으면 갱신한다.
- 사실, dist[3] + cost[3][4] = 26 > 20 = dist[4] 이므로 4번 정점까지의 거리(dist[4])는 갱신하지 않는다.
- 즉, 어떤 값도 갱신하지 않는다.
- 아직 방문하지 않은 정점 중 거리(dist 배열 값)가 가장 짧은 4번 정점을 방문한다.

| Vertex | 0 | 1 | 2 | 3 | 4 | 5 |
| Cost | 0 | 7 | 9 | 20 | 20 | 11 |
모든 정점을 방문했기 때문에 아무 것도 하지 않고 마무리한다.
다익스트라(Dijkstra) 알고리즘 코드 (C++)
#include <iostream>
#include <cstring>
#include <sstream>
#include <vector>
#include <deque>
#include <queue>
#include <map>
#include <algorithm>
#include <bitset>
#include <cmath>
#define INF (~0U >> 2) // 약 10억 7천만 (1073741823)
using namespace std;
int v, e, k; // 정점 개수, 간선 개수, 시작 정점
vector<pair<int, int>> adj[20001]; // 인접 리스트 (인접한 정점과 그 정점까지의 거리를 저장)
vector<int> dist(20001, INF);
// 우선순위 큐
// 큰 원소부터 pop : priority_queue<int> pq;
// 작은 원소부터 pop : priority_queue<int, vector<int>, greater<int>> pq;
void dijkstra(int start) { // start는 시작 정점
dist[start] = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq; // ({dist[k], k} 저장)
pq.push({ dist[k], k });
while (!pq.empty()) {
int cur_dist = pq.top().first;
int cur = pq.top().second;
pq.pop();
// 이미 방문한 정점은 무시 (이미 방문한 정점의 dist 값은 가장 최소인 상태)
if (dist[cur] < cur_dist) continue;
for (auto k : adj[cur]) {
int next_dist = k.first;
int next = k.second;
// 현재 정점을 거쳐서 인접 정점을 방문하는 것이 더 거리가 짧은 경우
// <=> dist[cur] + adj[cur][next] < dist[next]
if (cur_dist + next_dist < dist[next]) {
// 거리 갱신
dist[next] = cur_dist + next_dist;
pq.push({ dist[next], next });
}
}
}
}
int main(void) {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> v >> e >> k;
for (int i = 0; i < e; i++) {
int a, b, c; cin >> a >> b >> c;
adj[a].push_back({ c, b });
}
dijkstra(k);
for (int i = 1; i <= v; i++) {
if (dist[i] == INF) cout << "INF\n";
else cout << dist[i] << '\n';
}
return 0;
}위 코드는 백준 1753번 [최단 경로] 문제의 해답 코드이다.
https://www.acmicpc.net/problem/1753
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net
주의할 점
[주의점 1]
priority_queue의 원소로 pair<int, int>를 사용할 때 따로 비교 함수를 지정해주지 않는다면 first를 기준으로 정렬된다.
다익스트라 알고리즘에서는 priority_queue에서 정점 k에 대한 dist[k] 값이 여러 번 갱신된다면 priority_queue에 {dist[k], k} 쌍이 여러 개 존재할 수 있다.
그 여러 쌍 중에서, dist[k] 값이 작은 것이 더 앞으로 가도록 하기 때문에, 정렬 기준이 되는 dist 값을 first 위치에 두어야 한다.
pq.push({ dist[next], next });
그리고, dist[k] 값이 가장 작은 {dist[k], k} 쌍이 선택되어 정점 k에 방문하면, 말 그대로 dist[k] 값은 가능한 가장 최소의 값을 가지고 있는 상태이다.
그런데, priority_queue에 이제는 필요없는 {dist[k], k} 쌍들이 남아있을 수 있기 때문에, 이 쌍들을 무시하기 위해 다음과 같은 코드를 작성해주어야 한다.
if (dist[cur] < cur_dist) continue;
[주의점 2]
vector에서 큰 원소부터 접근하기 위해서는 내림차순 정렬 sort(v.begin(), v.end(), greater<>())을 하고,
작은 원소부터 접근하기 위해서는 오름차순 정렬 sort(v.begin(), v.end())을 한다.
비슷한 방식으로,
우선순위 큐에서 큰 원소부터 pop하기 위해서는 priority_queue<int> pq를 하고,
작은 원소부터 pop하기 위해서는 priority_queue<int, vector<int>, greater<int>> pq를 한다.
다음과 같이 이해하면 쉽게 기억할 수 있을 것이다.
vector는기존 그대로 생각하면 된다.
sort(v.begin(), v.end())를 하면 맨 앞에서부터, 즉 가장 작은 원소부터 접근하게 된다.

priority_queue는 vector를 세로로 세워서 생각하면 편하다.
그리고 맨 위에서부터 원소에 접근한다고 생각하면 된다.

즉, priority_queue<int> pq를 사용하면 우선 순위 큐에서 가장 큰 수부터 pop할 수 있다.
즉, vector와 priority_queue는 반대로 접근하면 된다.
'알고리즘 정리' 카테고리의 다른 글
| PS 문제 풀이 일지 (~ing) (0) | 2023.07.30 |
|---|---|
| 문자열 split 방법 (isstringstream 사용) (0) | 2023.05.12 |
